Description

给出一个正整数序列 a，长度为 n，cyb 不喜欢完美，他要删掉一些数（也可以不删，即删掉0个），但是他不会乱删，他希望删去以后，能将 a 分成 2 个集合，使得两个非空集合的数的和相同，现在他希望你能帮他算出删数的方案数。

Input

第一行 n 个正整数

以下有 n行，每行1个

正整数表示整数序列a

Output

一个整数表示答案

Sample Input

4

1 2 3 4

Sample Output

3

Hint

30%:n<=5

100%:n<=20

100%:a 中每个元素<=100000000

题解

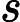
涉及到了hash，状压，双向搜索

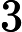
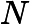首先可以想出一个3N的搜索．

枚举每个是不选还是在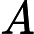A集合，还是在B集合

这样显然通不过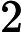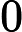20的数据

那么我们发现这个搜索是独立的

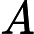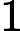
如果在A集合，我们令其为−1∗a

在B集合，令其为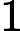1∗a

那么实际上我们在找一个方程有多少组解．

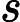
这样，我们先搜前面一半，将和用hash存起来

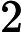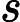
将选的情况，用一个2进制数也存入hash

这样可以通过全部数据

#include
     
      #include
      
       #include
       
        #include
        
         #include
         
          #include
          
           #define mod (100005)using namespace std;int n,a[21],lim,t[21];bool vis[1<<21];int head[100005],size,ans=0;struct hash{ int tot,st,next;}edge[100005];void add_hash(int tot,int st){ int key=(tot%mod+mod)%mod; size++; edge[size].tot=tot; edge[size].st=st; edge[size].next=head[key]; head[key]=size;}void find_hash(int tot,int st){ int key=(tot%mod+mod)%mod; for(int i=head[key];i!=-1;i=edge[i].next)if(edge[i].tot==tot)vis[edge[i].st+st]=1;}void dfs1(int k,int tot,int st){ if(k>lim) { add_hash(tot,st); return; } dfs1(k+1,tot,st); dfs1(k+1,tot+a[k],st+t[k]); dfs1(k+1,tot-a[k],st+t[k]);}void dfs2(int k,int tot,int st){ if(k==lim) { find_hash(tot,st); return; } dfs2(k-1,tot,st); dfs2(k-1,tot+a[k],st+t[k]); dfs2(k-1,tot-a[k],st+t[k]);}int main(){ freopen("regex.in","r",stdin); freopen("regex.out","w",stdout); memset(head,-1,sizeof(head)); int i,j; scanf("%d",&n);lim=n/2; for(i=1;i<=n;i++)scanf("%d",&a[i]),t[i]=1<<(i-1); dfs1(1,0,0); dfs2(n,0,0); int cnt=(1<<21)-1; for(i=1;i<=cnt;i++) ans+=vis[i]; printf("%d\n",ans); return 0;}